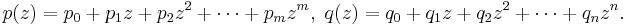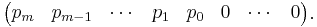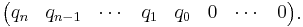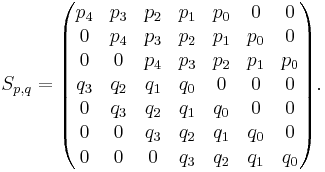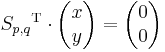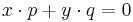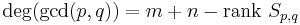Sylvester matrix

In mathematics, a Sylvester matrix is a matrix associated to two polynomials that provides information about those polynomials. It is named for James Joseph Sylvester.

1 Definition
2 Applications
3 See also
4 References
5 External links

Definition

Formally, let p and q be two nonzero polynomials, respectively of degree m and n. Thus:

$p(z)=p_0%2Bp_1 z%2Bp_2 z^2%2B\cdots%2Bp_m z^m,\;q(z)=q_0%2Bq_1 z%2Bq_2 z^2%2B\cdots%2Bq_n z^n.$

The Sylvester matrix associated to p and q is then the 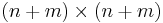$(n%2Bm)\times(n%2Bm)$ matrix obtained as follows:

the first row is:

$\begin{pmatrix} p_m & p_{m-1} & \cdots & p_1 & p_0 & 0 & \cdots & 0 \end{pmatrix}.$

the second row is the first row, shifted one column to the right; the first element of the row is zero.
the following (n-2) rows are obtained the same way, still filling the first column with a zero.
the (n+1)-st row is:

$\begin{pmatrix} q_n & q_{n-1} & \cdots & q_1 & q_0 & 0 & \cdots & 0 \end{pmatrix}.$

the following rows are obtained the same way as before.

Thus, if m=4 and n=3, the matrix is:

$S_{p,q}=\begin{pmatrix} p_4 & p_3 & p_2 & p_1 & p_0 & 0 & 0 \\ 0 & p_4 & p_3 & p_2 & p_1 & p_0 & 0 \\ 0 & 0 & p_4 & p_3 & p_2 & p_1 & p_0 \\ q_3 & q_2 & q_1 & q_0 & 0 & 0 & 0 \\ 0 & q_3 & q_2 & q_1 & q_0 & 0 & 0 \\ 0 & 0 & q_3 & q_2 & q_1 & q_0 & 0 \\ 0 & 0 & 0 & q_3 & q_2 & q_1 & q_0 \\ \end{pmatrix}.$

Applications

These matrices are used in commutative algebra, e.g. to test if two polynomials have a (non constant) common factor. In such a case, the determinant of the associated Sylvester matrix (which is named the resultant of the two polynomials) equals zero. The converse is also true.

The solutions of the simultaneous linear equations

${S_{p,q}}^\mathrm{T}\cdot\begin{pmatrix}x\\y\end{pmatrix} = \begin{pmatrix}0\\0\end{pmatrix}$

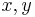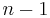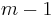where $x$ is a vector of size $n$ and $y$ has size $m$ , comprise the coefficient vectors of those and only those pairs $x, y$ of polynomials (of degrees $n-1$ and $m-1$ , respectively) which fulfill

$x \cdot p %2B y \cdot q = 0$

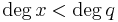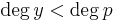(where polynomial multiplication and addition is used in this last line). This means the kernel of the transposed Sylvester matrix gives all solutions of the Bézout equation where $\deg x < \deg q$ and $\deg y < \deg p$ .

Consequently the rank of the Sylvester matrix determines the degree of the greatest common divisor of p and q.

$\deg(\gcd(p,q)) = m%2Bn-\mathrm{rank}~S_{p,q}$

References

Weisstein, Eric W., "Sylvester Matrix" from MathWorld.

External links

Additional overview

Sylvester matrix

Contents

Definition

Applications

See also

References

External links